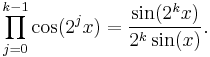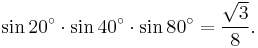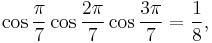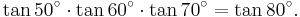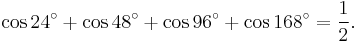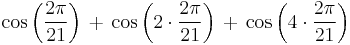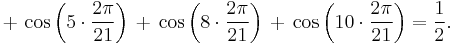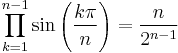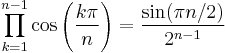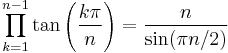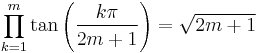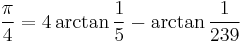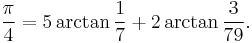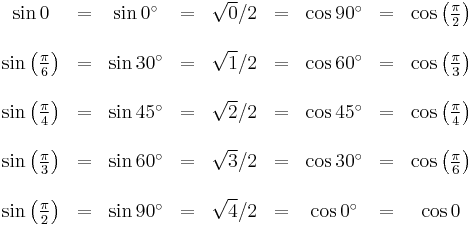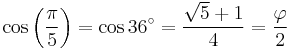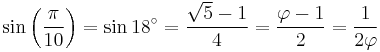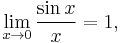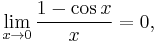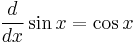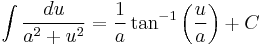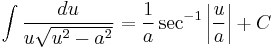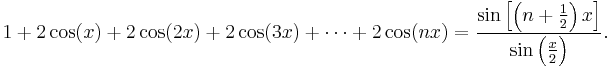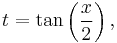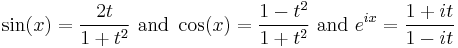List of trigonometric identities


| Trigonometry |
|---|
| History Usage Functions Generalized Inverse functions Further reading |
| Reference |
| Identities Exact constants Trigonometric tables |
| Laws and theorems |
| Law of sines Law of cosines Law of tangents Pythagorean theorem |
| Calculus |
| Trigonometric substitution Integrals of functions Derivatives of functions Integrals of inverse functions |
In mathematics, trigonometric identities are equalities that involve trigonometric functions and are true for every single value of the occurring variables (see Identity (mathematics)). Geometrically, these are identities involving certain functions of one or more angles. These are distinct from triangle identities, which are identities involving both angles and side lengths of a triangle. Only the former are covered in this article.
These identities are useful whenever expressions involving trigonometric functions need to be simplified. An important application is the integration of non-trigonometric functions: a common technique involves first using the substitution rule with a trigonometric function, and then simplifying the resulting integral with a trigonometric identity.
Notation
Angles
This article uses Greek letters such as alpha (α), beta (β), gamma (γ), and theta (θ) to represent angles. Several different units of angle measure are widely used, including degrees, radians, and grads:
- 1 full circle = 360 degrees = 2
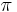 radians = 400 grads.
radians = 400 grads.
The following table shows the conversions for some common angles:
| Degrees | 30° | 60° | 120° | 150° | 210° | 240° | 300° | 330° |
|---|---|---|---|---|---|---|---|---|
| Radians | 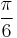 |
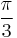 |
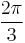 |
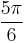 |
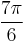 |
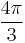 |
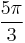 |
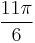 |
| Grads | 33⅓ grad | 66⅔ grad | 133⅓ grad | 166⅔ grad | 233⅓ grad | 266⅔ grad | 333⅓ grad | 366⅔ grad |
| Degrees | 45° | 90° | 135° | 180° | 225° | 270° | 315° | 360° |
| Radians | 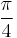 |
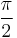 |
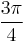 |
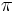 |
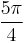 |
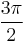 |
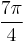 |
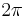 |
| Grads | 50 grad | 100 grad | 150 grad | 200 grad | 250 grad | 300 grad | 350 grad | 400 grad |
Unless otherwise specified, all angles in this article are assumed to be in radians, though angles ending in a degree symbol (°) are in degrees.
Trigonometric functions
The primary trigonometric functions are the sine and cosine of an angle. These are sometimes abbreviated sin(θ) and cos(θ), respectively, where θ is the angle, but the parentheses around the angle are often omitted, e.g., sin θ and cos θ.
The tangent (tan) of an angle is the ratio of the sine to the cosine:
Finally, the reciprocal functions secant (sec), cosecant (csc), and cotangent (cot) are the reciprocals of the cosine, sine, and tangent:
These definitions are sometimes referred to as ratio identities.
Inverse functions
The inverse trigonometric functions are partial inverse functions for the trigonometric functions. For example, the inverse function for the sine, known as the inverse sine (sin−1) or arcsine (arcsin or asin), satisfies
and
This article uses the following notation for inverse trigonometric functions:
| Function | sin | cos | tan | sec | csc | cot |
|---|---|---|---|---|---|---|
| Inverse | arcsin | arccos | arctan | arcsec | arccsc | arccot |
Pythagorean identity
The basic relationship between the sine and the cosine is the Pythagorean trigonometric identity:
where sin2x means (sin(x))2.
This can be viewed as a version of the Pythagorean theorem, and follows from the equation x2 + y2 = 1 for the unit circle. This equation can be solved for either the sine or the cosine:
Related identities
Dividing the Pythagorean identity through by either cos2 θ or sin2 θ yields two other identities:
Using these identities together with the ratio identities, it is possible to express any trigonometric function in terms of any other (up to a plus or minus sign):
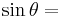 |
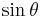 |
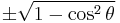 |
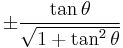 |
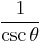 |
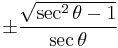 |
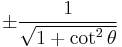 |
|---|---|---|---|---|---|---|
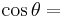 |
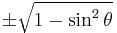 |
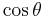 |
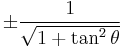 |
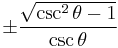 |
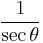 |
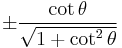 |
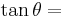 |
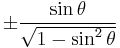 |
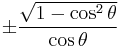 |
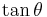 |
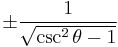 |
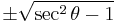 |
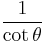 |
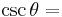 |
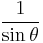 |
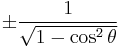 |
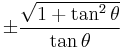 |
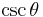 |
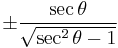 |
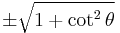 |
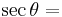 |
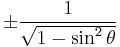 |
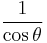 |
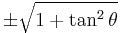 |
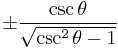 |
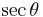 |
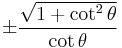 |
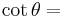 |
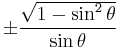 |
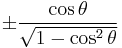 |
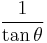 |
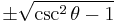 |
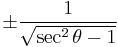 |
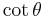 |
Historic shorthands
The versine, coversine, haversine, and exsecant were used in navigation. For example the haversine formula was used to calculate the distance between two points on a sphere. They are rarely used today.
| Name(s) | Abbreviation(s) | Value [2] |
|---|---|---|
| versed sine, versine | 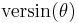 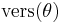 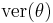 |
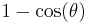 |
| versed cosine, vercosine | 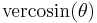 |
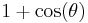 |
| coversed sine, coversine | 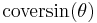 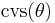 |
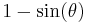 |
| coversed cosine, covercosine | 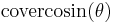 |
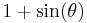 |
| haversed sine, haversine | 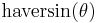 |
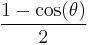 |
| haversed cosine, havercosine | 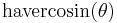 |
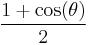 |
| hacoversed sine, hacoversine cohaversine |
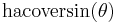 |
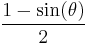 |
| hacoversed cosine, hacovercosine cohavercosine |
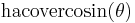 |
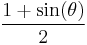 |
| exterior secant, exsecant | 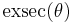 |
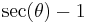 |
| exterior cosecant, excosecant | 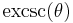 |
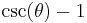 |
| chord | 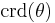 |
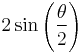 |
Symmetry, shifts, and periodicity
By examining the unit circle, the following properties of the trigonometric functions can be established.
Symmetry
When the trigonometric functions are reflected from certain angles, the result is often one of the other trigonometric functions. This leads to the following identities:
Reflected in 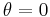 [3] [3] |
Reflected in 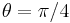 (co-function identities)[4] |
Reflected in 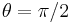 |
|---|---|---|
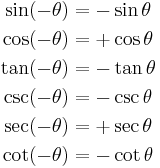 |
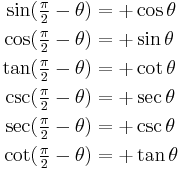 |
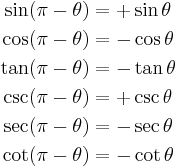 |
Shifts and periodicity
By shifting the function round by certain angles, it is often possible to find different trigonometric functions that express the result more simply. Some examples of this are shown by shifting functions round by π/2, π and 2π radians. Because the periods of these functions are either π or 2π, there are cases where the new function is exactly the same as the old function without the shift.
| Shift by π/2 | Shift by π Period for tan and cot[5] |
Shift by 2π Period for sin, cos, csc and sec[6] |
|---|---|---|
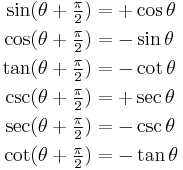 |
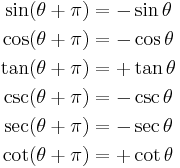 |
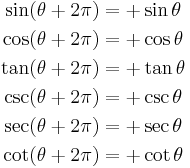 |
Angle sum and difference identities
These are also known as the addition and subtraction theorems or formulæ. They were originally established by the 10th century Persian mathematician Abū al-Wafā' Būzjānī. One method of proving these identities is to apply Euler's formula. The use of the symbols 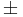 and
and 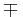 is described at the article Plus-minus sign.
is described at the article Plus-minus sign.
| Sine | 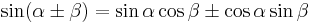 [7][8] [7][8] |
|---|---|
| Cosine | 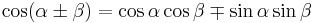 [8][9] [8][9] |
| Tangent | 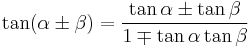 [8][10] [8][10] |
| Arcsine | 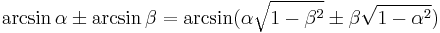 [11] [11] |
| Arccosine | 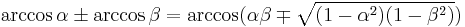 [12] [12] |
| Arctangent | 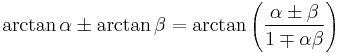 [13] [13] |
Matrix form
The sum and difference formulae for sine and cosine can be written in matrix form, thus:
Sines and cosines of sums of infinitely many terms
In these two identities an asymmetry appears that is not seen in the case of sums of finitely many terms: in each product, there are only finitely many sine factors and cofinitely many cosine factors.
If only finitely many of the terms θi are nonzero, then only finitely many of the terms on the right side will be nonzero because sine factors will vanish, and in each term, all but finitely many of the cosine factors will be unity.
Tangents of sums of finitely many terms
Let ek (for k ∈ {0, ..., n}) be the kth-degree elementary symmetric polynomial in the variables
for i ∈ {0, ..., n}, i.e.,
Then
the number of terms depending on n.
For example:
and so on. The general case can be proved by mathematical induction.
Secants of sums of finitely many terms
where ek is the kth-degree elementary symmetric polynomial in the n variables xi = tan θi, i = 1, ..., n, and the number of terms in the denominator depends on n.
For example,
Multiple-angle formulae
| Tn is the nth Chebyshev polynomial | 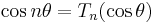 [14] [14] |
|---|---|
| Sn is the nth spread polynomial | 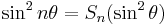 |
de Moivre's formula,  is the Imaginary unit is the Imaginary unit |
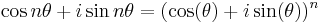 [15] [15] |
(This function of x is the Dirichlet kernel.)
Double-, triple-, and half-angle formulae
These can be shown by using either the sum and difference identities or the multiple-angle formulae.
| Double-angle formulae[16][17] | |||
|---|---|---|---|
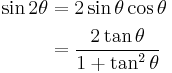 |
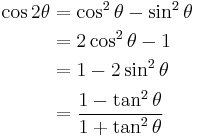 |
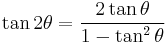 |
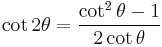 |
| Triple-angle formulae[14][18] | |||
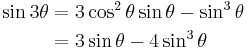 |
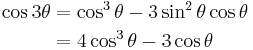 |
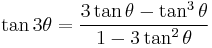 |
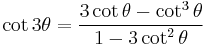 |
| Half-angle formulae[19][20] | |||
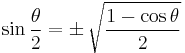 |
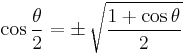 |
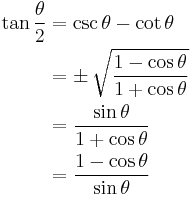 |
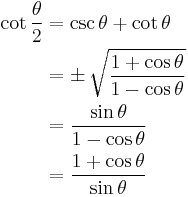 |
The fact that the triple-angle formula for sine and cosine only involves powers of a single function allows one to relate the geometric problem of a compass and straightedge construction of angle trisection to the algebraic problem of solving a cubic equation, which allows one to prove that this is in general impossible, by field theory.
A formula for computing the trigonometric identities for the third-angle exists, but it requires finding the zeroes of the cubic equation 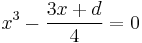 , where x is the value of the sine function at some angle and d is the known value of the sine function at the triple angle. However, the discriminant of this equation is negative, so this equation has three real roots (of which only one is the solution within the correct third-circle) but none of these solutions is reducible to a real algebraic expression, as they use intermediate complex numbers under the cube roots, (which may be expressed in terms of real-only functions only if using hyperbolic functions).
, where x is the value of the sine function at some angle and d is the known value of the sine function at the triple angle. However, the discriminant of this equation is negative, so this equation has three real roots (of which only one is the solution within the correct third-circle) but none of these solutions is reducible to a real algebraic expression, as they use intermediate complex numbers under the cube roots, (which may be expressed in terms of real-only functions only if using hyperbolic functions).
Sine, cosine, and tangent of multiple angles
For specific multiples, these follow from the angle addition formulas, while the general formula was given by 16th century French mathematician Vieta.
tan nθ can be written in terms of tan θ using the recurrence relation:
cot nθ can be written in terms of cot θ using the recurrence relation:
Chebyshev method
The Chebyshev method is a recursive algorithm for finding the nth multiple angle formula knowing the (n − 1)th and (n − 2)th formulae.[21]
The cosine for nx can be computed from the cosine of (n − 1) and (n − 2) as follows:
Similarly sin(nx) can be computed from the sines of (n − 1)x and (n − 2)x
For the tangent, we have:
where H/K = tan(n − 1)x.
Tangent of an average
Setting either α or β to 0 gives the usual tangent half-angle formulæ.
Viète's infinite product
Power-reduction formulae
Obtained by solving the second and third versions of the cosine double-angle formula.
| Sine | Cosine | Other |
|---|---|---|
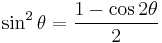 |
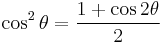 |
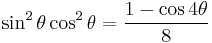 |
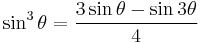 |
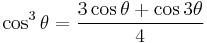 |
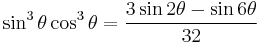 |
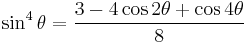 |
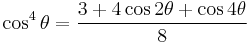 |
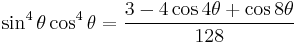 |
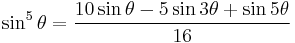 |
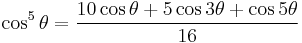 |
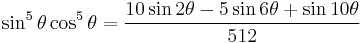 |
and in general terms of powers of sin θ or cos θ the following is true, and can be deduced using De Moivre's formula, Euler's formula and binomial theorem.
| Cosine | Sine | |
|---|---|---|
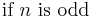 |
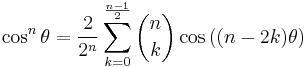 |
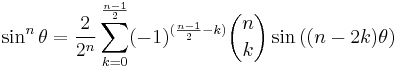 |
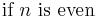 |
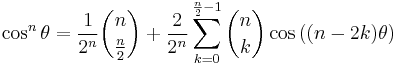 |
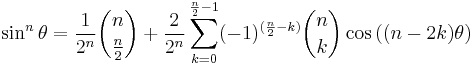 |
Product-to-sum and sum-to-product identities
The product-to-sum identities or prosthaphaeresis formulas can be proven by expanding their right-hand sides using the angle addition theorems. See beat (acoustics) for an application of the sum-to-product formulæ.
|
|
If x, y, and z are the three angles of any triangle, or in other words
(If any of x, y, z is a right angle, one should take both sides to be ∞. This is neither +∞ nor −∞; for present purposes it makes sense to add just one point at infinity to the real line, that is approached by tan(θ) as tan(θ) either increases through positive values or decreases through negative values. This is a one-point compactification of the real line.)
Hermite's cotangent identity
Charles Hermite demonstrated the following identity.[24] Suppose a1, ..., an are complex numbers, no two of which differ by an integer multiple of π. Let
(in particular, A1,1, being an empty product, is 1). Then
The simplest non-trivial example is the case n = 2:
Ptolemy's theorem
(The first three equalities are trivial; the fourth is the substance of this identity.) Essentially this is Ptolemy's theorem adapted to the language of trigonometry.
Linear combinations
For some purposes it is important to know that any linear combination of sine waves of the same period or frequency but different phase shifts is also a sine wave with the same period or frequency, but a different phase shift. In the case of a linear combination of a sine and cosine wave[25] (which is just a sine wave with a phase shift of π/2), we have
where
or equivalently
More generally, for an arbitrary phase shift, we have
where
and
Other sums of trigonometric functions
Sum of sines and cosines with arguments in arithmetic progression[26]:
For any a and b:
where atan2(y, x) is the generalization of arctan(y/x) which covers the entire circular range.
The above identity is sometimes convenient to know when thinking about the Gudermannian function, which relates the circular and hyperbolic trigonometric functions without resorting to complex numbers.
If x, y, and z are the three angles of any triangle, i.e. if x + y + z = π, then
Certain linear fractional transformations
If ƒ(x) is given by the linear fractional transformation
and similarly
then
More tersely stated, if for all α we let ƒα be what we called ƒ above, then
If x is the slope of a line, then ƒ(x) is the slope of its rotation through an angle of −α.
Inverse trigonometric functions
Compositions of trig and inverse trig functions
![\sin[\arccos(x)]=\sqrt{1-x^2} \,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ab24dbd6c097d578b9ba6d5ef8af13da.png) |
![\tan[\arcsin (x)]=\frac{x}{\sqrt{1 - x^2}}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/4005da685c90f33d145f122e34baaf66.png) |
![\sin[\arctan(x)]=\frac{x}{\sqrt{1+x^2}}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/e7b8c103e90d3201a10be0ddfe90a2cb.png) |
![\tan[\arccos (x)]=\frac{\sqrt{1 - x^2}}{x}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/7c4a9d034cd65dae312f3d4593636d40.png) |
![\cos[\arctan(x)]=\frac{1}{\sqrt{1+x^2}}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/65b8e718cbd943d44c5c0086c0cad02f.png) |
![\cot[\arcsin (x)]=\frac{\sqrt{1 - x^2}}{x}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/88435402b69aee3ce7c1e5f1ac715a4d.png) |
![\cos[\arcsin(x)]=\sqrt{1-x^2} \,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/a29cf2e566f9cc26ed2bb5b73337799e.png) |
![\cot[\arccos (x)]=\frac{x}{\sqrt{1 - x^2}}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/8ee9f8bedda57dd3f7c86e7e2f5049fe.png) |
Relation to the complex exponential function
and hence the corollary:
where  .
.
Infinite product formula
For applications to special functions, the following infinite product formulae for trigonometric functions are useful:[30][31]
|
|
|
Identities without variables
The curious identity
is a special case of an identity that contains one variable:
For example
A similar-looking identity is
Similarly:
The following is perhaps not as readily generalized to an identity containing variables (but see explanation below):
Degree measure ceases to be more felicitous than radian measure when we consider this identity with 21 in the denominators:
The factors 1, 2, 4, 5, 8, 10 may start to make the pattern clear: they are those integers less than 21/2 that are relatively prime to (or have no prime factors in common with) 21. The last several examples are corollaries of a basic fact about the irreducible cyclotomic polynomials: the cosines are the real parts of the zeroes of those polynomials; the sum of the zeroes is the Möbius function evaluated at (in the very last case above) 21; only half of the zeroes are present above. The two identities preceding this last one arise in the same fashion with 21 replaced by 10 and 15, respectively.
A lot of those curious identities stem from more general facts like the following [32]:
and
Combining these gives us
If n is an odd number (n = 2m+1) we can make use of the symmetries to get
Computing π
An efficient way to compute π is based on the following identity without variables, due to Machin:
or, alternatively, by using an identity of Leonhard Euler:
A useful mnemonic for certain values of sines and cosines
For certain simple angles, the sines and cosines take the form 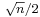 for 0 ≤ n ≤ 4, which makes them easy to remember.
for 0 ≤ n ≤ 4, which makes them easy to remember.
Miscellany
With the golden ratio φ:
Also see exact trigonometric constants.
Calculus
In calculus the relations stated below require angles to be measured in radians; the relations would become more complicated if angles were measured in another unit such as degrees. If the trigonometric functions are defined in terms of geometry, their derivatives can be found by verifying two limits. The first is:
verified using the unit circle and squeeze theorem. L'Hopital's rule can work as well: the derivative of sin x is cos x and the derivative of x is 1 so we find the wanted limit easily knowing that cos 0 = 1. The second limit is:
verified using the identity tan(x/2) = (1 − cos x)/sin x. Having established these two limits, one can use the limit definition of the derivative and the addition theorems to show that (sin x)′ = cos x and (cos x)′ = −sin x. If the sine and cosine functions are defined by their Taylor series, then the derivatives can be found by differentiating the power series term-by-term.
The rest of the trigonometric functions can be differentiated using the above identities and the rules of differentiation:[33][34][35]
The integral identities can be found in "list of integrals of trigonometric functions". Some generic forms are listed below.
Implications
The fact that the differentiation of trigonometric functions (sine and cosine) results in linear combinations of the same two functions is of fundamental importance to many fields of mathematics, including differential equations and Fourier transforms.
Exponential definitions
| Function | Inverse function[36] |
|---|---|
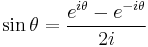 |
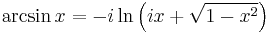 |
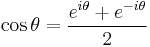 |
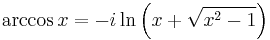 |
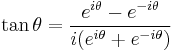 |
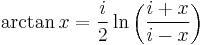 |
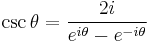 |
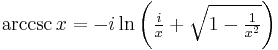 |
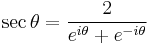 |
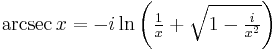 |
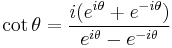 |
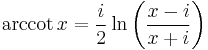 |
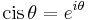 |
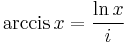 |
Miscellaneous
Dirichlet kernel
The Dirichlet kernel Dn(x) is the function occurring on both sides of the next identity:
The convolution of any integrable function of period 2π with the Dirichlet kernel coincides with the function's nth-degree Fourier approximation. The same holds for any measure or generalized function.
Extension of half-angle formula
If we set
then[37]
where eix = cos(x) + i sin(x), sometimes abbreviated to cis(x).
This substitution of t for tan(x/2), with the consequent replacement of sin(x) by 2t/(1 + t2) and cos(x) by (1 − t2)/(1 + t2) is useful in calculus for converting rational functions in sin(x) and cos(x) to functions of t in order to find their antiderivatives. For more information see tangent half-angle formula.
See also
- Trigonometry
- Proofs of trigonometric identities
- Uses of trigonometry
- Tangent half-angle formula
- Law of cosines
- Law of sines
- Law of tangents
- Half-side formula
- Mollweide's formula
- Pythagorean theorem
- Exact trigonometric constants (values of sine and cosine expressed in surds)
- Derivatives of trigonometric functions
- List of integrals of trigonometric functions
- Hyperbolic function
- Prosthaphaeresis
- Versine and haversine
- Exsecant
Notes
- ↑ Abramowitz and Stegun, p. 73, 4.3.45
- ↑ Abramowitz and Stegun, p. 78, 4.3.147
- ↑ Abramowitz and Stegun, p. 72, 4.3.13–15
- ↑ The Elementary Identities
- ↑ Abramowitz and Stegun, p. 72, 4.3.9
- ↑ Abramowitz and Stegun, p. 72, 4.3.7–8
- ↑ Abramowitz and Stegun, p. 72, 4.3.16
- ↑ 8.0 8.1 8.2 Weisstein, Eric W., "Trigonometric Addition Formulas" from MathWorld.
- ↑ Abramowitz and Stegun, p. 72, 4.3.17
- ↑ Abramowitz and Stegun, p. 72, 4.3.18
- ↑ Abramowitz and Stegun, p. 80, 4.4.42
- ↑ Abramowitz and Stegun, p. 80, 4.4.43
- ↑ Abramowitz and Stegun, p. 80, 4.4.36
- ↑ 14.0 14.1 Weisstein, Eric W., "Multiple-Angle Formulas" from MathWorld.
- ↑ Abramowitz and Stegun, p. 74, 4.3.48
- ↑ Abramowitz and Stegun, p. 72, 4.3.24–26
- ↑ Weisstein, Eric W., "Double-Angle Formulas" from MathWorld.
- ↑ Abramowitz and Stegun, p. 72, 4.3.27–28
- ↑ Abramowitz and Stegun, p. 72, 4.3.20–22
- ↑ Weisstein, Eric W., "Half-Angle Formulas" from MathWorld.
- ↑ Ken Ward's Mathematics Pages, http://www.trans4mind.com/personal_development/mathematics/trigonometry/multipleAnglesRecursiveFormula.htm
- ↑ Abramowitz and Stegun, p. 72, 4.3.31–33
- ↑ Abramowitz and Stegun, p. 72, 4.3.34–39
- ↑ Warren P. Johnson, "Trigonometric Identities à la Hermite", American Mathematical Monthly, volume 117, number 4, April 2010, pages 311–327
- ↑ Proof at http://pages.pacificcoast.net/~cazelais/252/lc-trig.pdf
- ↑ Michael P. Knapp, Sines and Cosines of Angles in Arithmetic Progression
- ↑ Abramowitz and Stegun, p. 74, 4.3.47
- ↑ Abramowitz and Stegun, p. 71, 4.3.2
- ↑ Abramowitz and Stegun, p. 71, 4.3.1
- ↑ Abramowitz and Stegun, p. 75, 4.3.89–90
- ↑ Abramowitz and Stegun, p. 85, 4.5.68–69
- ↑ Weisstein, Eric W., "Sine" from MathWorld
- ↑ Abramowitz and Stegun, p. 77, 4.3.105–110
- ↑ Abramowitz and Stegun, p. 82, 4.4.52–57
- ↑ Finney, Ross (2003). Calculus : Graphical, Numerical, Algebraic. Glenview, Illinois: Prentice Hall. pp. 159–161. ISBN 0-13-063131-0.
- ↑ Abramowitz and Stegun, p. 80, 4.4.26–31
- ↑ Abramowitz and Stegun, p. 72, 4.3.23
References
- Abramowitz, Milton; Stegun, Irene A., eds (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover Publications. ISBN 978-0-486-61272-0
External links
- Values of Sin and Cos, expressed in surds, for integer multiples of 3° and of 5⅝°, and for the same angles Csc and Sec and Tan.
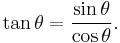
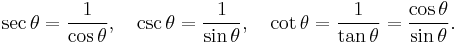
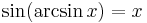
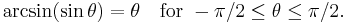
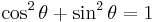
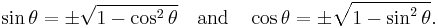
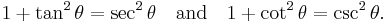
![\begin{align}
& {} \quad
\left(\begin{array}{rr}
\cos\phi & -\sin\phi \\
\sin\phi & \cos\phi
\end{array}\right)
\left(\begin{array}{rr}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{array}\right) \\[12pt]
& = \left(\begin{array}{rr}
\cos\phi\cos\theta - \sin\phi\sin\theta & -\cos\phi\sin\theta - \sin\phi\cos\theta \\
\sin\phi\cos\theta + \cos\phi\sin\theta & -\sin\phi\sin\theta + \cos\phi\cos\theta
\end{array}\right) \\[12pt]
& = \left(\begin{array}{rr}
\cos(\theta+\phi) & -\sin(\theta+\phi) \\
\sin(\theta+\phi) & \cos(\theta+\phi)
\end{array}\right)
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/5e498d1119eb6a7ae336a542a6ad2071.png)
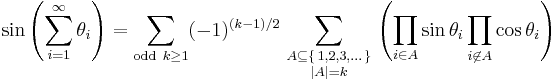
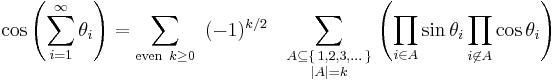
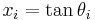
![\begin{align}
e_0 & = 1 \\[6pt]
e_1 & = \sum_{1 \le i \le n} x_i & & = \sum_{1 \le i \le n} \tan\theta_i \\[6pt]
e_2 & = \sum_{1 \le i < j \le n} x_i x_j & & = \sum_{1 \le i < j \le n} \tan\theta_i \tan\theta_j \\[6pt]
e_3 & = \sum_{1 \le i < j < k \le n} x_i x_j x_k & & = \sum_{1 \le i < j < k \le n} \tan\theta_i \tan\theta_j \tan\theta_k \\
& {}\ \ \vdots & & {}\ \ \vdots
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/fc69bc17e75c082f2a3e698d8e12fabf.png)
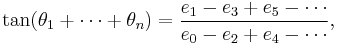
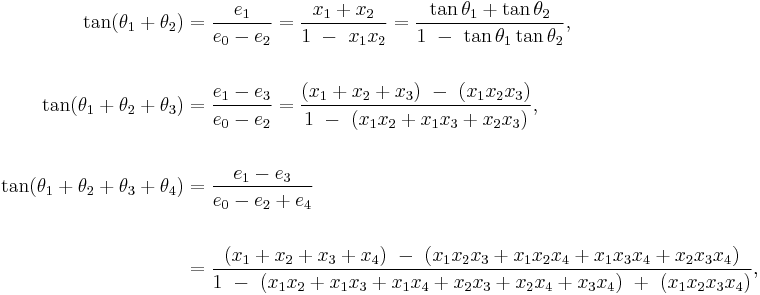
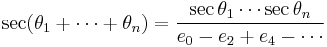
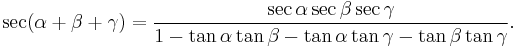
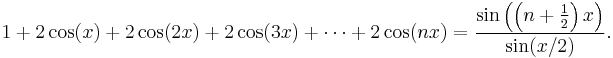
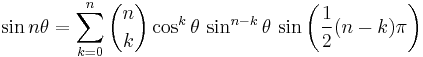
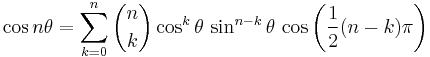
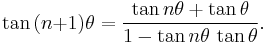
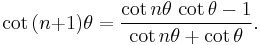
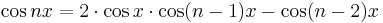
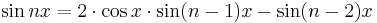
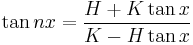
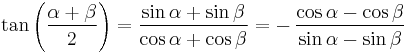
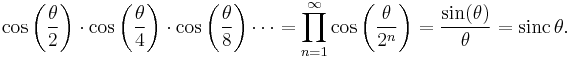
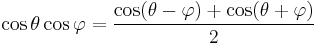
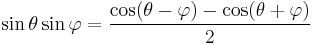
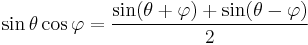
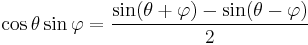
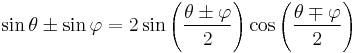
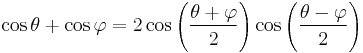
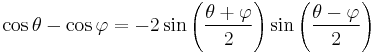
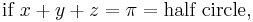
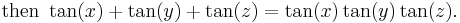
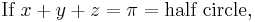
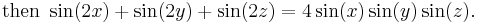
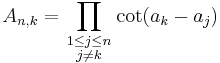
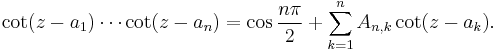
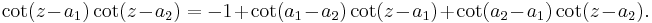
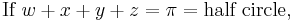
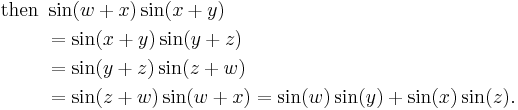
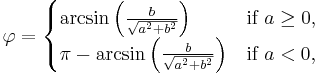
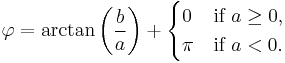
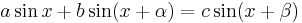
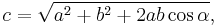
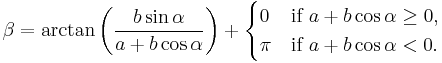
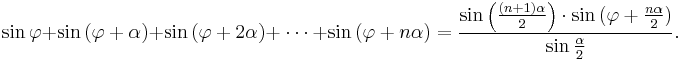
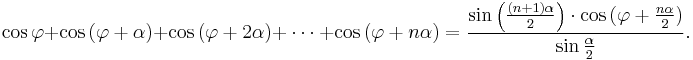
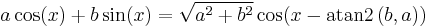
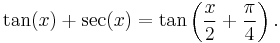
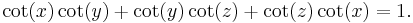
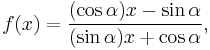
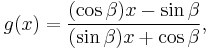
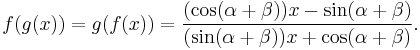
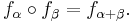
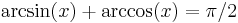
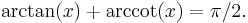
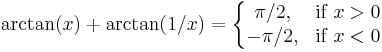
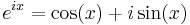
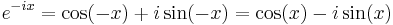
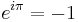 (
(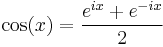
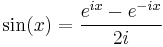
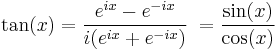
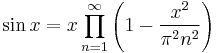
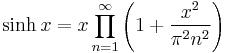
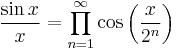
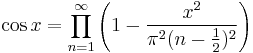
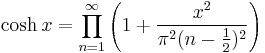
![|\sin x| = \frac1{2}\prod_{n = 0}^\infty \sqrt[2^{n+1}]{\left|\tan\left(2^n x\right)\right|}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ba74f68f504d35a32166a5b487410d82.png)